[BOJ] 백준 1004 어린왕자

https://www.acmicpc.net/problem/1004

1004번: 어린 왕자

1004 어린왕자 문제

해결사항:

만약에 이 문제가 최단거리를 요구했다면 더 어려웠을 것이다.

하지만 단순히 요구하는 것은 행성계 진입/이탈 의 횟수를 최소화 하는 경로를 찾는 것.

즉, 경로가 아무리 길어져도 행성계 진입/이탈 횟수만 적다면 된다는 뜻이다.

 

결국 이 문제는 출발점/도착점이 각각 몇개의 행성계에 속해있는가를 알아보는 것이다.

 

1. 모든 행성계를 순회하며, 출발점/도착점이 행성계 안에 존재하는지 확인한다.

 

    출발점/도착점이 행성계 밖에 있는 경우

1번 행성계

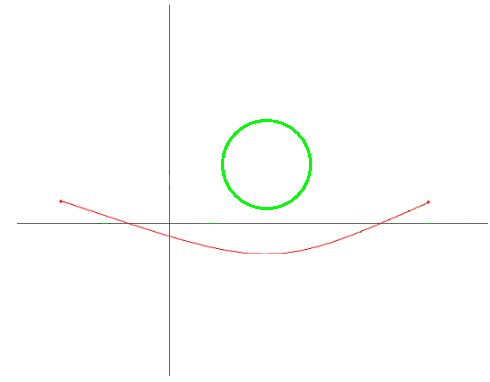
    이 경우에는 출발지/도착지가 1번 행성계를 진입/이탈 하지 않더라도 안전하게 도착지로 도착할 수 있다.

    따라서 1번 행성계는 진입/이탈에 대해 고려하지 않아도 된다.

 

2. 어떤 행성계 안에 출발점/도착점이 존재한다면, 3가지 경우를 고려할 수 있다.

1.  출발점은 행성계 안에 있지만, 도착점이 행성계 밖에 존재할 경우
   

   

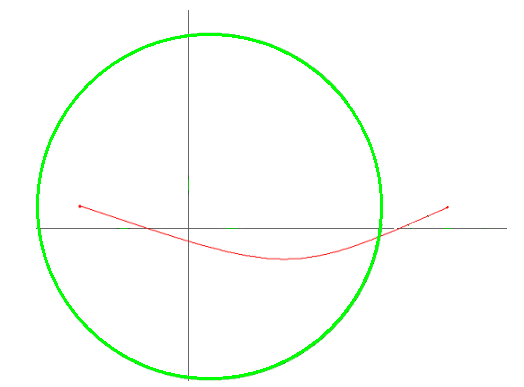
   2번 행성계

   이 경우에는 출발점이 행성계 안에 있지만, 도착점이 행성계 밖에 있다. 
   이런 경우에는 무조건 2번 행성계를 진입/이탈 해야한다.
   
   
2. 출발점은 행성계 밖에 있지만, 도착점이 행성계 안에 존재할 경우
   

   

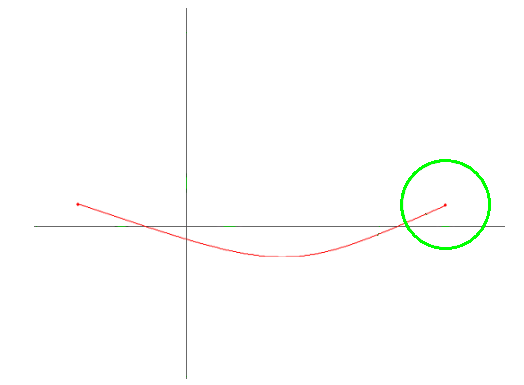
   3번 행성계

   이 경우에는 경우 1에서 출발점과 도착점이 바뀐것 뿐이다.
   역시 무조건 3번 행성계를 진입/이탈 해야한다.
   
   
3. 출발점/도착점이 같은 행성계 안에 있는 경우
   

   

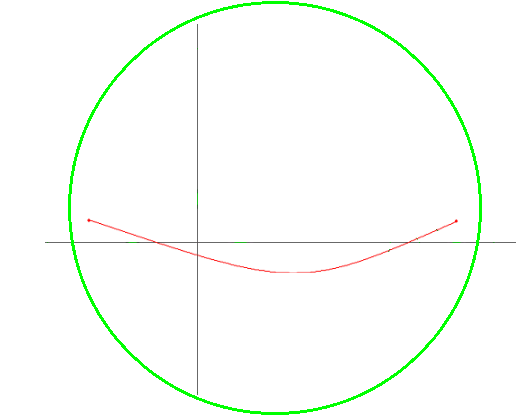
   4번 행성계

   이 경우에는 출발지/도착지가 같은 4번 행성계 안에 있기 때문에 이 행성계를 진입/이탈 하지 않아도
   안전하게 출발지로부터 도착지 까지 이동할 수 있다.

3. 위 경우들을 이용하여, 행성계를 진입/이탈 횟수를 조사한다.

 

코드:

 

#include <iostream>
#include <cmath>

double getDist(int x, int y, int t_x, int t_y){
	return sqrt(pow((x-t_x),2)+pow((y-t_y),2));
}
int main(){
	int T=0;
	std::cin>>T;
	// initialize answer array
	int answer[T]={0,};
	for(int i=0 ; i<T ; i++){
		// loop for test case
		int count = 0; 
		int startx, starty, endx, endy;
		std::cin>>startx>>starty>>endx>>endy;
		//std::cout<<"start_x: "<<startx<<" start_y: "<<starty<<" end_x: "<<endx<<" end_y: "<<endy;
		int N;
		std::cin>>N;
		int c_x, c_y, r;
		for(int j=0 ; j<N ; j++){
			std::cin>>c_x>>c_y>>r;
			double s_dist = getDist(startx, starty, c_x, c_y);
			double e_dist = getDist(endx, endy, c_x, c_y);
			if (s_dist<r && e_dist <r)
				;
			else if(s_dist<r)
				count++;
			else if(e_dist<r)
				count++;
		}
		answer[i]=count;

	}
	for(int elem: answer)
		std::cout<<elem<<std::endl;
	return 0;
}